Graph the Inequality: How to Plot Linear Inequalities on a Graph

by

Graphing inequalities is an essential skill in algebra and coordinate geometry. Whether you’re a student or someone brushing up on math fundamentals, understanding how to graph the inequality visually helps you solve problems involving conditions, ranges, and constraints.

In this guide, you’ll learn:

  • What an inequality is
  • How to convert an inequality into a graph
  • What shading means in the graph
  • How to handle strict and non-strict inequalities
  • Real-world examples to make it stick

Let’s walk through everything step by step.

Table of Contents

What Is an Inequality?

An inequality is a mathematical statement that compares two values using symbols like:

  • > (greater than)
  • < (less than)
  • ≥ (greater than or equal to)
  • ≤ (less than or equal to)

For example:

  • y > 2x + 1 means the y-values are above the line y = 2x + 1 (see the image below)
  • y ≤ -x + 3 includes all y-values on or below the line
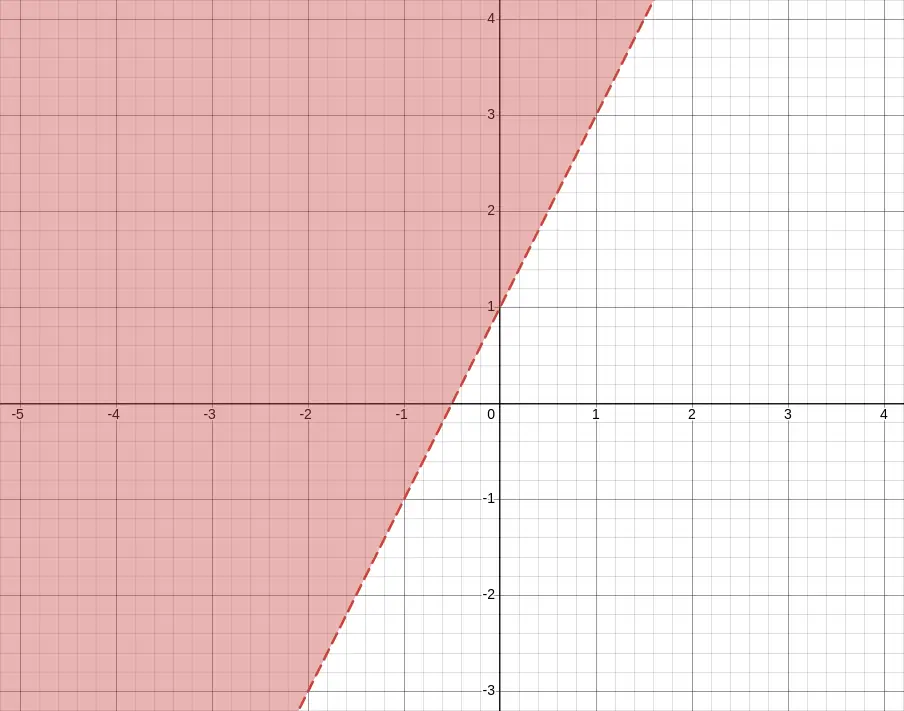
Graph the inequality example
Graph the Inequality Example: y > 2x + 1

How to Graph the Inequality

Here’s a simple process to follow when you want to graph the inequality:

1. Start with the Equation

Take the inequality and treat it like an equation for a moment.

Example:
y < 2x + 1
Graph the boundary line: y = 2x + 1

2. Draw the Boundary Line

  • If the inequality is < or >, use a dashed line
  • If it’s ≤ or ≥, use a solid line

This line separates the graph into two regions: one that satisfies the inequality and one that doesn’t.

3. Choose a Test Point

Pick a point that’s not on the line (usually the origin, (0, 0), works well unless the line passes through it).

Plug the test point into the original inequality:

  • If true, shade that side of the graph
  • If false, shade the other side

Example:
For y < 2x + 1, test (0, 0):
0 < 2(0) + 1 → 0 < 1 → True
So you shade below the line.

Graph the Inequality Examples

Example 1: y > x - 2

  1. Graph y = x - 2 (dashed line)
  2. Test point: (0, 0) → 0 > -2 → True
  3. Shade above the line

Example 2: y ≤ -0.5x + 3

  1. Graph y = -0.5x + 3 (solid line)
  2. Test point: (0, 0) → 0 ≤ 3 → True
  3. Shade below the line

Tips for Graphing Inequalities

  • Always rearrange into slope-intercept form (y = mx + b) first
  • Dashed = strict, Solid = inclusive
  • Use test points if you’re unsure where to shade
  • Check your shading direction after graphing to avoid errors

Graph the Inequality: Real-World Applications

Graphing inequalities is used in:

  • Budget constraints in economics
  • Feasibility regions in linear programming
  • Modeling safe ranges in science and engineering
  • Decision boundaries in machine learning

Tools to Help You Graph the Inequality

You can graph inequalities using:

  • Graphing calculators
  • Desmos (free online tool)
  • GeoGebra
  • Spreadsheet tools like Google Sheets or Excel (for simple inequality visuals)

How to Graph the Inequality Using Desmos

Desmos is a free online graphing calculator that makes it easy to plot linear inequalities visually. Here’s how to use it step by step:

1. Open Desmos

Visit the Desmos Graphing Calculator: https://www.desmos.com/calculator

You’ll see a blank graph on the right and input fields on the left.

2. Enter the Inequality

In one of the input boxes, type the inequality you want to graph. For example:

y < 2x + 3

Desmos will:

  • Draw a dashed line for < or > inequalities.
  • Use a solid line for ≤ or ≥ inequalities.
  • Automatically shade the region that represents all the solutions to the inequality.

The following image shows the example y < 2x + 3 in Desmos.

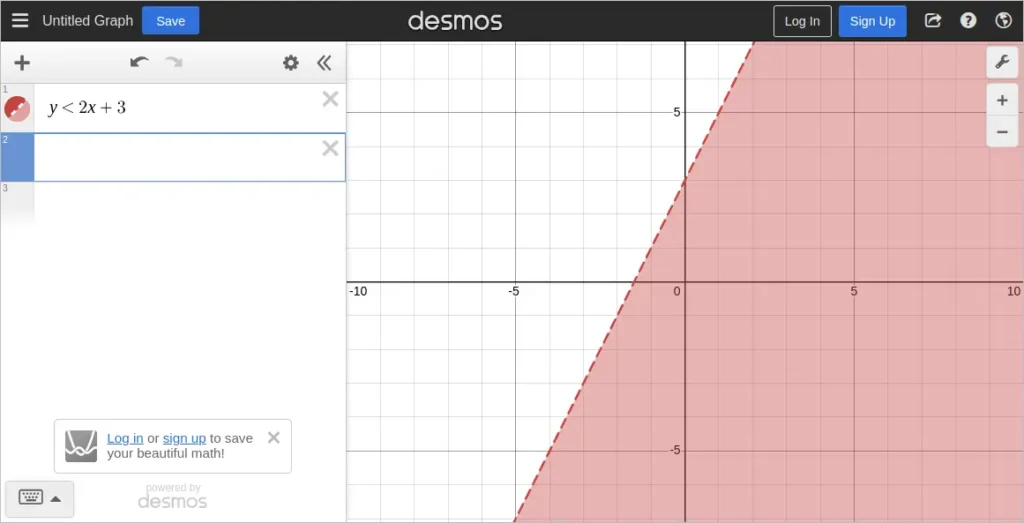
Graph the inequality shown in Desmos
Graph the Inequality y < 2x + 3 Shown in Desmos

3. Explore Other Inequality Types

Try typing in these variations to see how Desmos changes the graph:

  • y > 2x + 3 (shaded above, dashed line)
  • y ≤ 2x + 3 (shaded below, solid line)
  • y ≥ -x + 1 (shaded above, solid line)

You can also plot multiple inequalities to see overlapping solution areas, which is especially useful for solving systems.

4. Use Test Points (Optional)

If you’re unsure which area is shaded, you can add a test point (like (0, 0)) to the graph:

(0, 0)

This lets you visually confirm whether a specific point lies in the solution region.

Desmos is a powerful tool for students and teachers because it instantly shows the correct boundary line and shaded region. It also helps you avoid mistakes that might happen when drawing graphs by hand.

Final Thoughts on How to Graph the Inequality

Learning how to graph the inequality not only improves your math skills but also helps you solve real-world problems where constraints matter. By understanding boundary lines and shading regions correctly, you can quickly visualize where solutions exist and where they don’t.

You may be interested in our other graphing math functions.